El siguiente texto es una traducción del artículo First-class Everything de Guido van Rossum publicado en http://python-history.blogspot.com/.
Todo de primera clase
Uno de mis objetivos para Python era hacerlo de tal forma que todos los objetos sean de "primera clase". Con esto me refiero a que quería que todos los objetos puedan ser nombrados en el lenguaje (por ejemplo, enteros, strings, funciones, clases, módulos, métodos, etc.) para tener igual status. Entonces pueden ser asignados a variables, ubicados en listas, almacenados en diccionarios, pasados como argumentos y más.
La implementación interna de Python hizo que esto sea fácil de hacer. Todos los objetos de Python estaban basados en una estructura de datos de C común que se usaba en todos los lugares del intérprete. Variables, listas, funciones y todo lo demás usaba variaciones de esta estructura de datos; directamente no importaba si la estructura representaba un objeto simple como un entero o algo más complicado como una clase.
Aunque la idea de tener "todo de primera clase" es conceptualmente simple, había aún un aspecto de las clases que necesitaba resolver; el problema de hacer que los métodos sean objetos de primera clase.
Consideremos esta clase simple en Python (copiada de la entrada de la semana pasada):
class A:
def __init__(self,x):
self.x = x
def spam(self,y):
print self.x, y
Si los métodos van a ser objetos de primera clase, entonces pueden ser asignados a otras variables y usados como cualquier otro objeto en Python. Por ejemplo, alguien podría escribir una sentencia en Python como "s = A.spam". En este caso la variable "s" referencia un método de una clase, que en realidad es solo una función. Sin embargo, un método no es exactamente igual a una función. En concreto, se supone que el primer argumento de un método es una instancia de la clase en la que el método fue definido.
Para tratar esto cree un tipo de objeto invocable (callable) conocido como "unbound method". Un unbound method era en realidad un wrapper delgado alrededor de un objeto función que implementaba un método, pero forzaba la restricción de que el primer argumento tenía que ser una instancia de la clase en la cual el método fue definido. Así, si alguien quería llamar al unbound method "s" como una función, tendrían que pasar una instancia de la clase "A" como primer argumento. Por ejemplo, "a = A(); s(a)".(*)
Un problema relacionado ocurre si alguien escribe una sentencia Python que refiere al método en una instancia específica de un objeto. Por ejemplo, alguien puede crear una instancia usando "a = A()" y luego escribir una sentencia como "s = a.spam". Aquí la variable "s" nuevamente referencia al método de una clase, pero la referencia a ese método se obtuvo a través de la instancia "a". Para manejar esta situación se usa un objeto invocable diferente llamado "bound method". Este objeto es también un wrapper delgado alrededor del objeto función para el método. Sin embargo, este envoltorio implícitamente almacena la instancia original que fue usada para obtener el método. Así, una sentencia futura como "s()" llamará al método implícitamente con la instancia "a" como el primer argumento.
En realidad el mismo objeto interno es usado para representar los bound y unbound methods. Uno de los atributos de este objeto contiene una referencia a una instancia. Si es None, el método es unbound. De otro modo, el método es bound.
A pesar de que bound y unbound methods parezcan un detalle sin importancia, son una parte crítica de como las clases funcionan bajo el tapete. Siempre que una sentencia como "a.spam()" aparece en un programa, la ejecución de la sentencia ocurre en dos partes. Primero ocurre la búsqueda de "a.spam". Esto retorna un bound method; un objeto invocable. Luego, una operación de llamado de función "()" es aplicada a ese objeto para invocar el método con los argumentos provistos por el usuario.
(*) En Python 3000, el concepto de unbound methods se eliminó y la expresión "A.spam" retorna un objeto función normal. Nos dimos cuenta de que la restricción de que el primer argumento sea una instancia de A ayudaba pocas veces al diagnosticar problemas y frecuentemente era un obstáculo para usos avanzados; alguien lo llamó "duck typing self", el cual parece un nombre apropiado.
Traducido por Juan José Conti.
Revisado por César Portela.
Si encontrás errores en esta traducción, por favor reportalos en un comentario y los corregiremos a la brevedad.
Todas las traducciones de esta serie pueden encontrarse en La historia de Python.
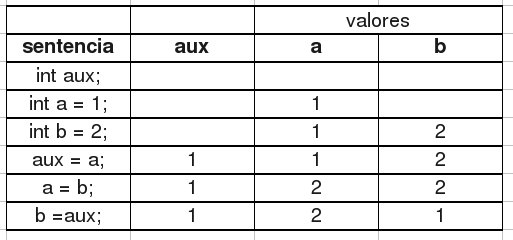
 La forma correcta de intercambiar los valores habría sido utilizando una variable auxiliar en la cual mantener uno de los valores:
La forma correcta de intercambiar los valores habría sido utilizando una variable auxiliar en la cual mantener uno de los valores: